This blog post gives a basic introduction to coordinate systems and projections, with a focus on UK data. To seasoned geographers, I apologise for all the things I’ve simplified or simply left out! My intention is to provide GIS novices who are a bit confused by the topic with just enough about various different coordinate systems to get started working with them in ArcGIS. Anyone looking for an excellent comprehensive introduction should refer to Ordnance Survey’s guide.
A coordinate system lets us define where a location is in space. In GIS, there are many types of coordinate systems, of which the two most used are geographic (3D) and projected (2D). The difference is shown below:
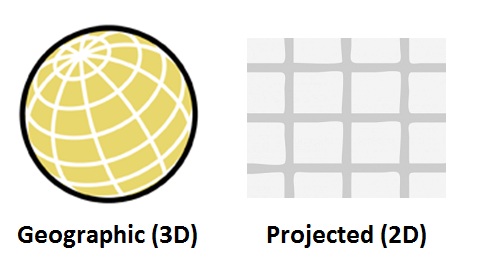
A geographic coordinate system (GCS) uses a grid on the surface of a 3D globe (the technical term for this grid is graticule; the North/South lines are lines of longitude and the East/West lines are lines of latitude). Graticule lines are not parallel to each other because they are defined using angles (e.g. degrees) from the centre of the globe, not linear units (e.g. metres) on a flat surface.
A projected coordinate system (PCS) is a flattened version of a 3D coordinate system. Grid lines are parallel, and coordinates are given in “flat” units like metres or feet. Although the Earth isn’t flat, we often use flat surfaces to represent it (paper surfaces, computer screens, etc), so we frequently need to convert 3D coordinates to 2D coordinates. However, there’s a problem: imagine peeling the skin off an orange and trying to make it sit flat on a table. It’s not possible to do this without ripping or stretching the peel! It’s the same with a 3D coordinate system. Whenever we flatten, or “project”, a 3D coordinate grid to a 2D coordinate grid, we have to distort the grid’s proportions somehow. Distances, shapes, areas, and angles, or some combination of all four, are deformed.
If you work with UK data, there are two geographic and two projected coordinate systems that you should know about. They are shown in the diagram below, along with the numeric WKID (Well-Known ID) of that GCS/PCS, as well as their relationships with one another and example coordinates in each system showing the location of Esri UK’s head office in Aylesbury.
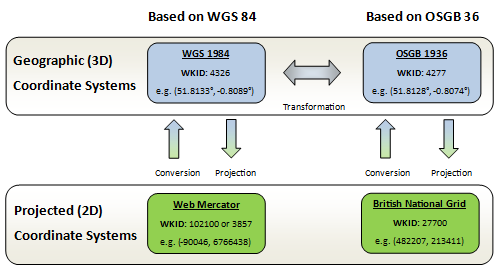
World Geodetic System (WGS-84) is familiar to many non-geographers because it is used by GPS devices to describe locations all over the Earth. A different GCS, called OSGB-36, which is more accurate for describing locations in Britain but not as good for other countries, is used specifically for British data. Web Mercator is a PCS based on WGS-84 used for global maps, and British National Grid is a PCS based on OSGB-36 used for British maps.
For each GCS, there are many different ways of converting, or “projecting”, 3D coordinates to 2D coordinates. Web Mercator and British National Grid are the most important projections for their respective geographic coordinate systems. There are alternative projections, each with its own pros and cons.
Converting between coordinate systems that are based on the same GCS is relatively straightforward, but when converting, for example, GPS (WGS-84) coordinates to BNG eastings and northings, a mathematical transformation is required. The “Petroleum” transformation is an accurate transformation from WGS-84 to OSGB-36 (and vice-versa) included with ArcGIS.
To convert data between WGS-84 and BNG in ArcGIS Desktop, you should use the Project tool. Make sure you select the “Petroleum” transformation otherwise your results will not be accurate.
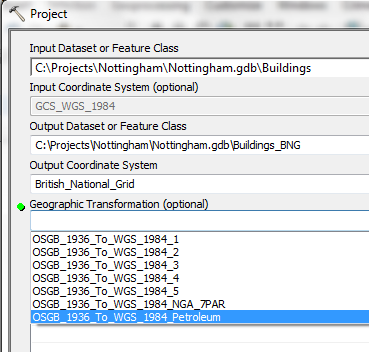
Select the optional Petroleum transformation for the best results
For GB data, you only really need to know about WGS-84 and BNG, and that you should use the Petroleum transformation to get an accurate conversion between them. You will also need to use “Petroleum” to convert between BNG/OSGB-36 and Web Mercator (or WGS 1984 Web Mercator Auxiliary Sphere, to give it the name used by Esri). Web Mercator has become the standard projection for international consumer web maps, such as Google Maps, Bing Maps, and OpenStreetMap. All ArcGIS Online basemaps are also in this projection.